İlk olan her zaman kazanmaz

Son iki haftadır üzerinde çalıştığımız Penney oyununda, diğerlerinden üstün bir üçlü olmadığı için (geçişsizlik ilkesinin özü budur), ikinciyi seçmek daha iyidir, çünkü diğer kişi ne seçerse seçsin, kazanma olasılığı her zaman daha yüksek olan bir üçlü olacaktır. Basitçe söylemek gerekirse, taş-kağıt-makas oyununda aynı anda değil de art arda seçim yapabiliyormuşuz gibi: ikinciyi seçen kişinin her zaman kazanacağı aşikar.

Penney'nin oyununda, ikinci oyuncunun stratejisi (taş-kağıt-makas oyunundaki gibi başarı garantisi olmasa da olasılıksal olarak daha avantajlıdır), ilk terimi diğer oyuncunun üçlüsünün ikinci teriminin tersi olan ve ikinci ve üçüncü terimleri sırasıyla diğer oyuncunun üçlüsünün birinci ve ikinci terimleri olan üçlüyü seçmektir. Örneğin, ilk oyuncu XXC üçlüsünü seçerse, ikinci oyuncu CXX'i seçmelidir. (Notunu yükseltmek için bunun en iyi strateji olduğunu gösterin.)

Atipik zar

Grime'ın zarları hakkında Salva Fuster şöyle diyor: "Her bir zara bir harf atarsak:

A: 4 4 4 4 4 9

B: 3 3 3 3 8 8

C: 2 2 2 7 7 7

Gün: 1 1 6 6 6 6

E: 0 5 5 5 5 5

A'nın, B ve C'ye karşı kazandığını, ancak D ve E'ye kaybettiğini; B'nin, C ve D'ye karşı kazandığını, ancak E ve A'ya kaybettiğini ve bu şekilde devam ettiğini biliyoruz. A, B, C, D ve E köşelerinden oluşan bir beşgen çizersek, her köşe sonraki ikisine karşı kazanır ve önceki ikisine kaybeder. Şimdi, bu tam olarak bir kazanç değil, ancak kazanma olasılığı daha yüksek. Örneğin, A zarı B'ye karşı 10'a kıyasla 26 kez kazanırken, B, C'ye karşı 12'ye kıyasla 24 kez kazanır. Her zarın diğerlerine karşı kazanma veya kaybetme olasılığını hesaba katarsak, hepsi ikisine karşı kazanıp diğer ikisine kaybetse bile, A veya D zarını seçmenin daha iyi olduğunu söyleyebilirim, çünkü diğer zarlardan kazanma olasılıkları biraz daha fazladır.

Üç tane daha geçişsiz zar var. Her birinin üzerindeki noktaların toplamı, geleneksel zarlarda olduğu gibi 21'e eşit ve puanlar bunlar gibi 1 ile 6 arasında değişiyor. Ayrıca, T zarı olmadıkları için her zar diğer ikisinden birine karşı kazanır, diğerine karşı kaybeder. Yüzlerinde hangi sayılar görünüyor?

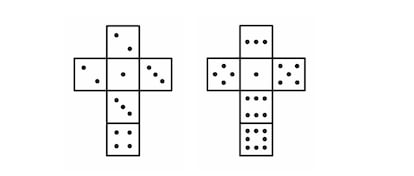
Sicherman zarları hakkında Bretos Bursó şöyle diyor: "Tüm yüzlerin pozitif sayılar olduğunu varsayarsak, alışılmış olan 123456, 123456'nın dışında yalnızca bir çözüm vardır, ancak bazı yüzlerin 0 puana sahip olmasına izin verirsek daha fazla çözüm vardır: en küçük yüzleri 1 ve 1 olan bir çözüm verildiğinde, bir zarın her yüzünden bir puan çıkarıp diğer zarın yüzlerine bir puan eklersek, başka bir çözüm elde edilir. Örneğin, alışılmış çözüm 012345, 234567 sonucunu verir. 0 olmadan diğer çözümü elde etmek için, şu gözlemlerden başladım: iki en küçük yüz 1 ve 1 olmalı ve iki en büyük yüz 12'ye kadar toplanmalı; her zarda en küçük ve en büyük yüzler tekrarlanamaz; ve tüm yüzlerin toplamı 42 olmalı, böylece her zarda ne en küçük ne de en büyük olan sekiz yüzün toplamı 28 olmalıdır.

Bu gözlemlerden şeklin çözümünü elde ederiz: 122334, 134568. Bunun tek olduğunu kanıtlayabilir misiniz?