Leonardo's world map

The area of ​​the Reuleaux triangle (R) from last week is equal to that of the equilateral triangle with side 1 (T) plus three times that of the circular segment (S) on each side:

R = T + 3S, where S is the circular sector minus the triangle:

S = π/6 – T, then

R = T + 3(π/6 – T) = π/2 – 2T

T = √3/4

R = (π - √3)/2

Some readers have pointed out that there are also coins shaped like Reuleaux polygons. The best known is undoubtedly the British 50p coin, which is a Reuleaux heptagon.

The answer to the question of whether there can be Reuleaux polygons (i.e., polygons of constant width) constructed from some irregular polygons or polygons with an even number of sides, posed last week, is affirmative; but in this case the arcs of the resulting polygon will not all be the same or have the same curvature.

One of the lesser-known, but no less important, aspects of Leonardo da Vinci's work is his contribution to cartography. In his miscellany, the Codex Atlanticus , housed in the Ambrosian Library in Milan, there is a 1508 manuscript in which Leonardo analyzes the various types of map projections known at the time, such as Ptolemy's planar conic projection and the Contarini-Rosselli planisphere, and introduces a new one. This new projection consists of dividing the globe into eight octants and then flattening them into Reuleaux triangles. Was this an arbitrary or purely aesthetic choice, or does flattening an octant of a sphere necessarily produce a Reuleaux triangle?

Leonardo grouped the four octants of each hemisphere forming a kind of four-leaf clover, with the poles in the respective centers of each clover, giving rise to what is known as the "Leonardo World Map," although its authorship is not certain (some think that it was drawn later by one of his assistants); but what is solidly demonstrated is that the Renaissance genius was the first to propose the projection in octants and their grouping into two four-leaf clovers, as attested, among other things, by a sketch of the aforementioned 1508 manuscript included in the Codex Atlanticus .

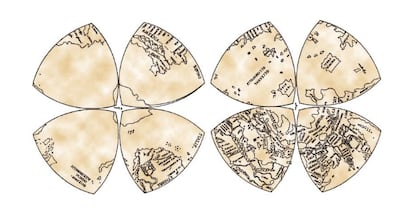
It should be noted that the octant projection is neither conformal nor equal-area. In cartography, a conformal projection preserves angles (or at least most of them), such as the Mercator or stereographic projections, while an equal-area projection preserves the proportions of the areas of different countries or other geographical regions represented. Other characteristics that may be desirable to preserve, depending on the type of map being created, are the shape of different geographical areas, distances, directions, etc., and sometimes preserving one of these variables means distorting others. Can a map projection be both conformal and equal-area? How?

And, to conclude, I pose to my astute readers a question that, although it may seem botanical, is purely logical: Are there four-leaf clovers?