Вопросы с подвохом

Ни один читатель не пожелал продемонстрировать, что 7 «бесконечных» сигарет прошлой недели находятся в полном контакте — все они друг с другом — и не предложил иного решения, кроме представленного. Вот еще один:

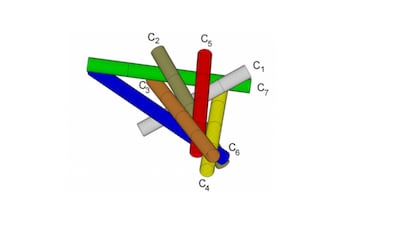
Снова возникает вопрос, что некоторые контакты очевидны, а другие — менее очевидны. Как, например, доказать, что сигареты С1 и С2 соприкасаются?

Что касается растянутой пружины , вот что комментирует Франциско Монтесинос: «Если радиус витков r остается постоянным во время растяжения из-за большого сопротивления кривизне пружины, возникает противоречие, потому что если шаг деформированной спирали равен py и если мы рассмотрим пружину с одним витком, ее длина будет √[(2pi.r)^2+p^2], а не (2pi.r), как можно было бы подумать. Можно справедливо утверждать, что этот последний r — это r', отличный от предыдущего r, но тогда мы должны пояснить , что радиус, который может оставаться постоянным во время растяжения, — это радиус цилиндрической оболочки пружины, а не катушки».

Правосудие и математика

Ссылки на коэффициент Пуассона в последние недели вызвали ряд комментариев относительно работы французского математика по применению исчисления вероятностей к оценке судебных ошибок. В 1837 году Симон-Дени Пуассон опубликовал эссе под названием «Исследования вероятности судебных процессов по уголовным и гражданским делам». Это была не первая попытка применить исчисление вероятностей к оценке судебных разбирательств: в 1785 году маркиз де Кондорсе опубликовал свой труд «О применении анализа к вероятности решений, выносимых на основе множественности голосов», а Пьер-Симон Лаплас в своем «Философском опыте о вероятности» (1814) также попытался рассчитать вероятность того, что решение, вынесенное в ходе судебного разбирательства, будет правильным. Главным вкладом Пуассона стало введение в его анализ доступных статистических данных и закона больших чисел для определения предполагаемой частоты события, например, ошибочного предложения, за определенный период времени. Его работа не получила одобрения ни в юридической, ни в научной сфере, хотя в конечном итоге она выявила его заметный методологический интерес. Но это уже другая статья.

Вопросы и препятствия

За последние несколько недель мы увидели несколько примеров «приготовленных» загадок и вопросов с подвохом, что кажется хорошим поводом предложить несколько (и, возможно, некоторые из них можно будет приготовить). Хотя простое предупреждение о том, что вопросы «каверзные», снижает их эффективность, вам все равно нужно быть осторожным, чтобы не попасть в одну из следующих ситуаций:

1. За четыре последовательных года в скольких месяцах 31 день, в скольких — 30 дней и в скольких — 28 дней?

2. Всегда ли вопрос, единственно возможный ответ на который вам известен заранее, является лишним?

3. Какая гора была самой высокой в ​​мире до того, как ее назвали Эверестом?

4. Почему большинство собак спят больше часов в январе, чем в феврале?

5. Какое животное охотится на мышей, мяукает и царапается, но не является кошкой?

6. Что произойдет, если непреодолимая сила столкнется с неподвижным объектом? (Как забавно, я впервые столкнулся с этим вопросом в детстве, прочитав комикс, в котором Супермен путешествует во времени и врезается сам в себя.)