Это кажется невозможным…

Существуют математические задачи , которые кажутся разрешимыми, но таковыми не являются, например, квадратура круга, и другие, которые кажутся невозможными, но могут быть решены с помощью небольшого нестандартного мышления. Среди последних, одна из самых известных, о которой мы уже говорили, — это задача о девяти точках, расположенных в сетке 3x3, которые нужно соединить четырьмя прямыми, не отрывая карандаш от бумаги и не пересекая одну и ту же линию дважды. Другая, недавно обсуждавшаяся задача — тупоугольный треугольник , который нужно разделить на острые углы.

В обоих случаях кажущаяся невозможность связана с тем, что, не осознавая этого, мы накладываем на себя больше условий, чем следует из условия. В задаче о 9 точках мы предполагаем, что все вершины ломаной, соединяющей точки, должны совпадать с некоторыми из точек, чего от нас не требуется. Но как насчёт сетки 4x4 , каким количеством прямых, по крайней мере, можно соединить все точки, не отрывая карандаш от бумаги и не пересекая одну и ту же линию дважды? А в сетках 5x5, 6x6 и т. д.? Существует ли формула, позволяющая определить количество прямых по количеству точек?

Что касается предполагаемой невозможности деления тупоугольного треугольника на острые углы ( Мартин Гарднер рассказал мне, что однажды он получил несколько «демонстраций» того, что такое деление невозможно), то это происходит из-за похожего ложного предположения: мы склонны думать, что все вершины острых углов должны находиться на периметре тупого угла, а это не обязательно так.

Движущаяся часть

На прошлой неделе наш постоянный комментатор Сальва Фустер предложила интересную задачу, похожую на две предыдущие (хотя на первый взгляд она может показаться не связанной, она также относится к классу задач с обманом). Суть её в следующем:

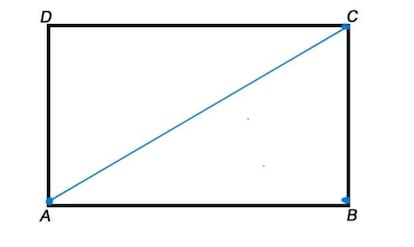
Начертим прямоугольник ABCD. Расставим фигуры в точках A, B и C (образуя прямоугольный треугольник ABC), которые можно перемещать. Чтобы переместить любую из фигур, она должна быть параллельна прямой, образованной положением двух других фигур. Сколько ходов потребуется, чтобы две из трёх фигур оказались посередине двух сторон прямоугольника ABCD? И чтобы все три фигуры заняли свои места?

Точка Фейербаха

Вернёмся к окружности девяти точек. Как отмечает Луис Ортис: «Поскольку точки D, F и H являются серединами отрезков IA, IB и IC, треугольник DFH получается путём применения к треугольнику ABC растяжения с центром I и отношением сторон 1/2. То есть, DFH — треугольник, подобный ABC, но вдвое меньше [см. соответствующий рисунок в предыдущей публикации]. И то же растяжение справедливо для окружностей, описанных вокруг обоих треугольников, включая их центры. Следовательно, центр окружности девяти точек будет находиться в середине отрезка, соединяющего ортоцентр I с центром описанной окружности треугольника ABC».

И мы не можем попрощаться с окружностью девяти точек, не упомянув точку Фейербаха, которая является точкой касания указанной окружности с вписанной окружностью рассматриваемого треугольника.

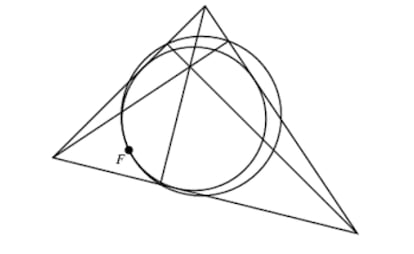
Окружность девяти точек , свойства которой кажутся неисчерпаемыми, также касается трёх вписанных окружностей (касающихся каждой стороны и продолжений двух других). Можете ли вы вычислить длины радиусов вписанных окружностей треугольника со сторонами 3, 4 и 5?

Наконец (пока что тема неисчерпаема), точки касания окружности девяти точек с тремя вписанными окружностями являются вершинами так называемого треугольника Фейербаха . Но это тема другой статьи.