Il triangolo di Reuleaux

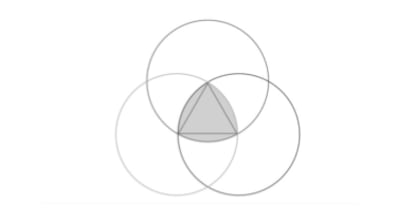
Se, dato un triangolo equilatero, tracciamo cerchi con centri nei tre vertici e raggio uguale al lato del triangolo, l'intersezione di questi cerchi è un triangolo di Reuleaux, dal nome dell'ingegnere tedesco Franz Reuleaux (1829-1905), considerato il padre della cinematica. (Sapete calcolarne l'area, prendendo come unità di misura il lato del triangolo equilatero?)

Il triangolo di Reuleaux è la figura a larghezza costante più semplice dopo, ovviamente, il cerchio . E, come sottolinea AlienJ Campo in risposta alla domanda della scorsa settimana: "Altre forme per i tombini che impedirebbero la caduta attraverso il foro potrebbero essere il triangolo di Reuleaux o altri poligoni dello stesso tipo, sebbene sarebbero meno pratici sia per la costruzione che per la chiusura del foro, perché non ruoterebbero sul bordo del supporto con la stessa facilità".

Una figura di larghezza costante è quella che, se la racchiudiamo tra due linee parallele tangenti ad essa, la distanza tra tali linee parallele è sempre la stessa, indipendentemente dalla posizione della figura.

Il triangolo di Reuleaux, sebbene il suo studio cinematico e le sue applicazioni meccaniche siano dovuti all'ingegnere che gli diede il nome, è noto fin dall'antichità. Leonardo da Vinci lo utilizzò nella sua proiezione ottante (ma questo è un altro argomento) e lo ritroviamo nelle vetrate gotiche di alcune chiese, tra cui la Sagrada Familia.

Con qualsiasi poligono regolare con un numero dispari di lati, possiamo realizzare una costruzione simile a quella del triangolo di Reuleaux tracciando una circonferenza da ciascun vertice attraverso i due vertici del lato opposto. Otteniamo così i vari poligoni di Reuleaux, anch'essi di larghezza costante e, quindi, candidati per i tombini. E non solo tombini: esistono persino biciclette le cui ruote sono poligoni di Reuleaux (vi vengono in mente dei vantaggi che potrebbero avere rispetto alle ruote circolari?).

Perché non esistono poligoni di Reuleaux regolari con un numero pari di lati? Oppure sì? È possibile ottenere figure di larghezza costante da poligoni irregolari?

Per quanto riguarda le possibili forme di spade rinfoderabili, oltre alla spada a lama dritta e alla sciabola la cui curvatura è un arco di cerchio, potrebbe essere rinfoderata anche una spada elicoidale; tuttavia, questa spada a cavatappi non sembra molto pratica.

Il becco dell'anfora

La particolare forma delle anfore romane ha suscitato molti dibattiti tra i miei gentili lettori , soprattutto a causa della loro punta appuntita, che a prima vista sembra poco pratica. Tuttavia, questo beccuccio solido e molto robusto permetteva di maneggiare le anfore con una certa ruvidità. Forniva un solido appoggio quando le si appoggiava a terra e potevano persino essere trascinate senza grande sforzo e senza timore di romperle (l'enorme numero di anfore romane sopravvissute intatte fino ad oggi è impressionante). Inoltre, il beccuccio fungeva da terza maniglia per sollevarle e versarne il contenuto. E, ultimo ma non meno importante, quando le anfore venivano riposte nella stiva di una nave, che era il loro consueto mezzo di trasporto, i beccucci di una fila venivano incastrati tra i colli e le anse di un'altra fila, ottenendo così uno stivaggio compatto e stabile.