Domande trabocchetto

Nessun lettore è stato disposto a dimostrare che le 7 sigarette "infinite" della scorsa settimana siano in pieno contatto, tutte tra loro, né ha proposto una soluzione diversa da quella presentata. Eccone un altro:

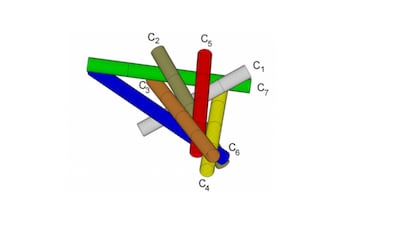
Ritorna la domanda: alcuni contatti sono evidenti, altri meno. Come possiamo dimostrare, ad esempio, che le sigarette C1 e C2 si toccano?

Riguardo alla molla tesa , ecco cosa commenta Francisco Montesinos: "Se il raggio delle spire r rimane costante durante l'allungamento a causa di una grande resistenza alla curvatura della molla, sorge una contraddizione, perché se il passo dell'elica deformata è py e se consideriamo la molla con una sola spira, la sua lunghezza sarà √[(2π.r)^2+p^2] e non (2π.r) come si potrebbe pensare. Si può giustamente sostenere che quest'ultimo r è un r' diverso dal precedente r, ma allora dovremmo chiarire che il raggio che può rimanere costante durante l'allungamento è quello dell'involucro cilindrico della molla, non quello della spira."

Giustizia e matematica

I riferimenti al coefficiente di Poisson nelle ultime settimane hanno suscitato numerosi commenti in merito al lavoro del matematico francese sull'applicazione del calcolo delle probabilità alla valutazione degli errori giudiziari. Nel 1837, Simon-Denis Poisson pubblicò un saggio intitolato Recherches sur la probabilité des jugements en matière criminelle et en matière civile (Indagini sulla probabilità dei processi in materia penale e civile). Non si trattava del primo tentativo di applicare il calcolo delle probabilità alla valutazione di procedimenti giudiziari: il marchese di Condorcet, nel 1785, aveva pubblicato il suo Saggio sull'applicazione dell'analisi alla probabilità delle decisioni rese alla pluralità delle voci, e anche Pierre-Simon Laplace, nel suo Saggio filosofico sulla probabilità (1814), aveva tentato di calcolare la probabilità che la sentenza emessa in un processo fosse corretta. Il contributo principale di Poisson fu quello di introdurre i dati statistici disponibili e la legge dei grandi numeri nelle sue analisi per determinare la frequenza stimata di un evento (ad esempio, una frase errata) in un dato periodo di tempo. Il suo lavoro non fu ben accolto né in ambito giudiziario né in quello scientifico, nonostante avrebbe finito per rivelare il suo notevole interesse metodologico. Ma questo è un altro articolo.

Domande e ostacoli

Nelle ultime settimane abbiamo visto alcuni esempi di enigmi "costruiti" e domande trabocchetto, il che ci sembra una buona scusa per suggerirne alcuni (e forse alcuni di essi saranno realizzabili). Anche se limitarsi ad avvertire che le domande sono “difficili” ne diminuisce l’efficacia, bisogna comunque fare attenzione a non inciampare in nessuno dei seguenti punti:

1. In quattro anni consecutivi, quanti mesi hanno 31 giorni, quanti ne hanno 30 e quanti ne hanno 28?

2. Una domanda di cui conosci in anticipo l'unica possibile risposta è sempre superflua?

3. Qual era la montagna più alta del mondo prima che si conoscesse il monte Everest?

4. Perché la maggior parte dei cani dorme più ore a gennaio che a febbraio?

5. Quale animale caccia i topi, miagola e graffia, ma non è un gatto?

6. Cosa succede se una forza irresistibile entra in collisione con un oggetto immobile? (Per raccontarvi un curioso aneddoto, mi sono posto per la prima volta questa domanda durante la mia infanzia, leggendo un fumetto in cui Superman viaggia nel tempo e si schianta contro se stesso.)