Questions pièges

Aucun lecteur n'a voulu démontrer que les 7 cigarettes « infinies » de la semaine dernière sont en contact total – toutes entre elles – ni n'a proposé une solution autre que celle présentée. En voici un autre :

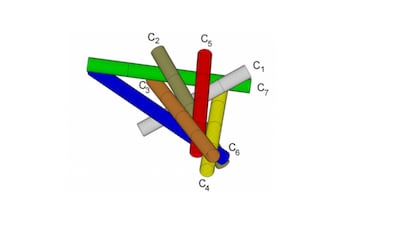
La question se pose à nouveau : certains contacts sont évidents, mais d’autres le sont moins. Comment peut-on prouver, par exemple, que les cigarettes C1 et C2 se touchent ?

Concernant le ressort étiré , voici ce que Francisco Montesinos commente : « Si le rayon des spires r reste constant pendant l’allongement en raison d’une grande résistance à la courbure du ressort, une contradiction apparaît, car si le pas de l’hélice déformée est py et si l’on considère le ressort à une seule spire, sa longueur sera √[(2pi.r)^2+p^2] et non (2pi.r) comme on pourrait le penser. On peut à juste titre affirmer que ce dernier r est un r' différent du précédent r, mais il convient alors de préciser que le rayon qui peut rester constant pendant l’allongement est celui de l’enveloppe cylindrique du ressort, et non celui de la spire. »

Justice et mathématiques

Les références au coefficient de Poisson ont suscité ces dernières semaines un certain nombre de commentaires concernant les travaux du mathématicien français sur l'application du calcul des probabilités à l'évaluation des erreurs judiciaires. En 1837, Simon-Denis Poisson publie un essai intitulé Recherches sur la probabilité des jugements en matière criminelle et en matière civile. Ce n'était pas la première tentative d'appliquer le calcul des probabilités à l'évaluation des procédures judiciaires : le marquis de Condorcet avait publié en 1785 son Essai sur l'application de l'analyse à la probabilité des décisions rendues à la pluralité des voix, et Pierre-Simon Laplace, dans son Essai philosophique sur la probabilité (1814), avait également tenté de calculer la probabilité que le jugement rendu dans un procès soit correct. La principale contribution de Poisson a été d’introduire les données statistiques disponibles et la loi des grands nombres dans ses analyses pour déterminer la fréquence estimée d’un événement – ​​par exemple, une phrase erronée – dans une période de temps donnée. Ses travaux ne furent pas bien accueillis, ni dans les sphères judiciaires ni dans les sphères scientifiques, même s'ils révéleraient par la suite son intérêt méthodologique notable. Mais c'est un autre article.

Questions et obstacles

Au cours des dernières semaines, nous avons vu quelques exemples d'énigmes et de questions pièges « cuisinées », ce qui semble être une bonne excuse pour en suggérer quelques-unes (et peut-être que certaines d'entre elles seront cuisinées). Même si le simple fait d’avertir que les questions sont « délicates » diminue leur efficacité, vous devrez néanmoins faire attention à ne pas tomber dans l’un des cas suivants :

1. Au cours de quatre années consécutives, combien de mois ont 31 jours, combien en ont 30 et combien en ont 28 ?

2. Une question dont on connaît à l’avance la seule réponse possible est-elle toujours superflue ?

3. Quelle était la plus haute montagne du monde avant qu’on ne sache qu’il s’agissait du mont Everest ?

4. Pourquoi la plupart des chiens dorment-ils plus d’heures en janvier qu’en février ?

5. Quel animal chasse les souris, miaule et griffe, mais n’est pas un chat ?

6. Que se passe-t-il si une force irrésistible entre en collision avec un objet immobile ? (Pour une anecdote curieuse, j'ai été confronté à cette question pour la première fois, dans mon enfance, dans une bande dessinée dans laquelle Superman voyage dans le temps et se percute lui-même.)